杂志(Magazine)
INTERNATIONAL JOURNAL OF EPIDEMIOLOGY
中科院SCI期刊分区( 2017最新版本)—医学·一区TOP,IF:7.738
背景(Introduction)
这篇文章旨在介绍环境流行病学中常用的一种研究设计–时间序列回归。这种研究通常用于定量评估环境暴露因素(如空气污染、花粉、粉尘、气象因素)与健康结局之间的短期关系。
数据特征(Data features)
library(foreign)
data <- read.dta("C:/Users/Administrator/Desktop/dyt092/ije-2012-10-0989-File003.dta")
rbind(head(data),tail(data))
## date ozone temperature relative_humidity numdeaths
## 1 2002-01-01 4.586225 -0.22500001 75.67830 199
## 2 2002-01-02 4.876853 0.08749995 77.52500 231
## 3 2002-01-03 4.707875 0.85000002 81.32500 210
## 4 2002-01-04 4.137461 0.53750002 85.45000 203
## 5 2002-01-05 2.005846 4.25000000 93.52500 224
## 6 2002-01-06 2.401446 7.06874990 96.40000 198
## 1821 2006-12-26 10.090909 5.47193909 83.80000 162
## 1822 2006-12-27 5.818182 5.47891951 85.47500 153
## 1823 2006-12-28 23.181818 7.93744278 85.85000 157
## 1824 2006-12-29 37.727272 8.00941944 88.02500 153
## 1825 2006-12-30 56.818180 9.73178577 84.20000 143
## 1826 2006-12-31 56.363636 10.01869106 85.52499 137
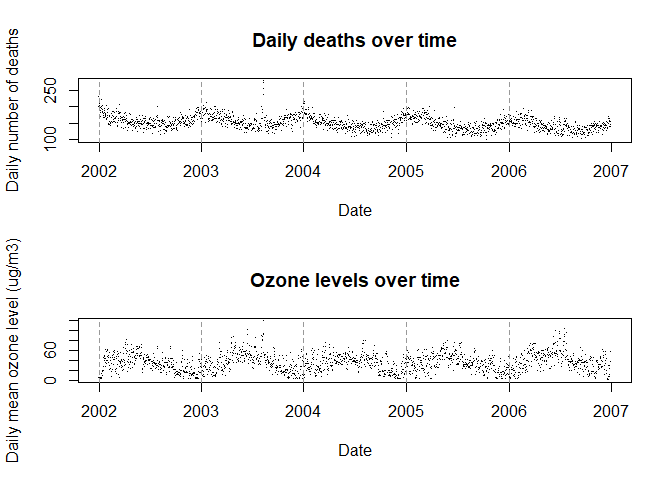
该数据集包含伦敦2002-1-1至2006-12-31每天的臭氧、温度、相对湿度和死亡人数数据。这种研究设计强调的是“臭氧的逐日变异是否与每日的死亡风险有关”?这种时间序列数据存在以下特征:
-
“时间序列”一般是以固定时间间隔记录的一系列数据点,该数据集实际包含四个时间序列。
-
时间序列分析单位(每行数据)是“天”,并不是“个体”。注意时间序列回归分析时间间隔不一定都是每日水平,也可能是每年、每月 、每周,甚至每小时。
-
时间序列回归分析的结局变量通常是计数资料。
描述性分析(Descriptive analysis)
时间序列分析的第一步通常是通过简单的图表来了解数据,如绘制散点图:
options(na.action="na.exclude")
# FIGURE 1
# SET THE PLOTTING PARAMETERS FOR THE PLOT (SEE ?par)
oldpar <- par(no.readonly=TRUE)
par(mex=0.8,mfrow=c(2,1))
# SUB-PLOT FOR DAILY DEATHS, WITH VERTICAL LINES DEFINING YEARS
plot(data$date,data$numdeaths,pch=".",main="Daily deaths over time",
ylab="Daily number of deaths",xlab="Date")
abline(v=data$date[grep("-01-01",data$date)],col=grey(0.6),lty=2)
# THE SAME FOR OZONE LEVELS
plot(data$date,data$ozone,pch=".",main="Ozone levels over time",
ylab="Daily mean ozone level (ug/m3)",xlab="Date")
abline(v=data$date[grep("-01-01",data$date)],col=grey(0.6),lty=2)
par(oldpar)
layout(1)
其他描述性分析:
# SUMMARY
summary(data)
## date ozone temperature relative_humidity
## Min. :2002-01-01 Min. : 1.182 Min. :-1.401 Min. :31.23
## 1st Qu.:2003-04-02 1st Qu.: 21.091 1st Qu.: 7.506 1st Qu.:58.69
## Median :2004-07-01 Median : 34.922 Median :11.473 Median :69.61
## Mean :2004-07-01 Mean : 34.772 Mean :11.720 Mean :69.10
## 3rd Qu.:2005-09-30 3rd Qu.: 46.725 3rd Qu.:16.198 3rd Qu.:80.36
## Max. :2006-12-31 Max. :119.246 Max. :28.175 Max. :98.86
## numdeaths
## Min. : 99.0
## 1st Qu.:135.0
## Median :148.0
## Mean :149.5
## 3rd Qu.:162.0
## Max. :280.0
# CORRELATIONS
cor(data[,2:4])
## ozone temperature relative_humidity
## ozone 1.0000000 0.4560300 -0.5269955
## temperature 0.4560300 1.0000000 -0.4442078
## relative_humidity -0.5269955 -0.4442078 1.0000000
时间序列回归(Time series regression)
经过初步的描述性分析,接下来就是建立回归模型(泊松回归)。
回归分析目标
回归的主要目标是研究结局的短期变异能否被主要暴露的改变所解释。在该例子中,即死亡人数的逐日改变能否部分被臭氧变化所解释。回归同样需要控制潜在的混在因素。
使用泊松回归进行分析
对于结局变量是计数资料的回归分析,通常选用泊松回归。这类时间序列数据还存在几个特殊点:
-
在这个例子的原始数据中,可以看到明显的长期趋势及季节性。
-
原始数据不满足泊松回归的一个假设:观测值并非完全独立的,相邻时间的观测值比较远时间间隔的更为相似。这种自相关是由解释变量引起的,通过控制长期趋势、季节性、暴露因素及其他混杂因素,残差自相关会明显变小。
-
结局变量本身的变异大于泊松分布的预测值,因此在建模时有必要进行细微的调整。
控制长期趋势及季节性
主要介绍三种控制长期趋势及季节性的方法:
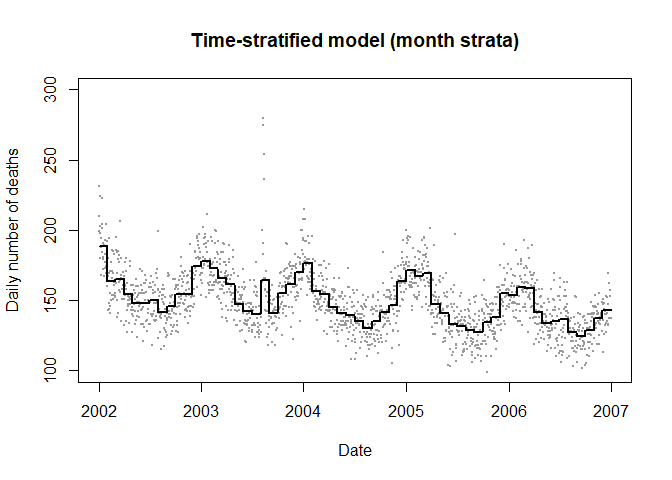
时间分层模型(Time stratified model)
一种简单的方法就是讲研究区间分为更为细小的区间,并分别估计每个小区间的死亡风险,实际操作可以按照自然月进行拆分,如本数据可以分为12 × 5 = 60层。
优点:易于理解,长期趋势也能较好把握。
缺点:产生大量潜在的模型参数;隐式的假定了相邻时间间隔存在跳跃式的死亡风险。
# OPTION 1: TIME-STRATIFIED MODEL
# (SIMPLE INDICATOR VARIABLES)
# GENERATE MONTH AND YEAR
data$month <- as.factor(months(data$date,abbr=TRUE))
data$year <- as.factor(substr(data$date,1,4))
# FIT A POISSON MODEL WITH A STRATUM FOR EACH MONTH NESTED IN YEAR
# (USE OF quasipoisson FAMILY FOR SCALING THE STANDARD ERRORS)
model1 <- glm(numdeaths ~ month/year,data,family=quasipoisson)
summary(model1)
##
## Call:
## glm(formula = numdeaths ~ month/year, family = quasipoisson,
## data = data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.8334 -0.7629 -0.0403 0.7076 8.1611
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.041342 0.016999 296.562 < 2e-16 ***
## month11月 -0.003091 0.024259 -0.127 0.898615
## month12月 0.121045 0.023345 5.185 2.41e-07 ***
## month1月 0.197499 0.022938 8.610 < 2e-16 ***
## month2月 0.057217 0.024313 2.353 0.018714 *
## month3月 0.066166 0.023653 2.797 0.005207 **
## month4月 -0.004173 0.024266 -0.172 0.863489
## month5月 -0.043040 0.024303 -1.771 0.076741 .
## month6月 -0.045707 0.024526 -1.864 0.062545 .
## month7月 -0.028773 0.024215 -1.188 0.234912
## month8月 -0.090068 0.024601 -3.661 0.000258 ***
## month9月 -0.057050 0.024599 -2.319 0.020497 *
## month10月:year2003 0.001251 0.024033 0.052 0.958508
## month11月:year2003 0.045016 0.024205 1.860 0.063085 .
## month12月:year2003 -0.028108 0.022789 -1.233 0.217607
## month1月:year2003 -0.059053 0.022109 -2.671 0.007631 **
## month2月:year2003 0.055558 0.024248 2.291 0.022066 *
## month3月:year2003 0.002729 0.023242 0.117 0.906543
## month4月:year2003 0.045477 0.024215 1.878 0.060543 .
## month5月:year2003 -0.005239 0.024596 -0.213 0.831347
## month6月:year2003 -0.039573 0.025254 -1.567 0.117297
## month7月:year2003 -0.068855 0.024820 -2.774 0.005592 **
## month8月:year2003 0.152715 0.024241 6.300 3.75e-10 ***
## month9月:year2003 -0.036478 0.025378 -1.437 0.150785
## month10月:year2004 -0.088017 0.024587 -3.580 0.000353 ***
## month11月:year2004 -0.050998 0.024794 -2.057 0.039846 *
## month12月:year2004 -0.066660 0.023015 -2.896 0.003822 **
## month1月:year2004 -0.063968 0.022137 -2.890 0.003904 **
## month2月:year2004 -0.047157 0.024657 -1.913 0.055970 .
## month3月:year2004 -0.069927 0.023676 -2.954 0.003183 **
## month4月:year2004 -0.059746 0.024863 -2.403 0.016364 *
## month5月:year2004 -0.052061 0.024890 -2.092 0.036609 *
## month6月:year2004 -0.060681 0.025391 -2.390 0.016959 *
## month7月:year2004 -0.108250 0.025076 -4.317 1.67e-05 ***
## month8月:year2004 -0.082747 0.025685 -3.222 0.001298 **
## month9月:year2004 -0.079758 0.025662 -3.108 0.001913 **
## month10月:year2005 -0.140137 0.024928 -5.622 2.19e-08 ***
## month11月:year2005 -0.112931 0.025197 -4.482 7.87e-06 ***
## month12月:year2005 -0.119586 0.023336 -5.124 3.31e-07 ***
## month1月:year2005 -0.095105 0.022317 -4.262 2.14e-05 ***
## month2月:year2005 0.021358 0.024452 0.873 0.382536
## month3月:year2005 0.022390 0.023129 0.968 0.333147
## month4月:year2005 -0.044471 0.024766 -1.796 0.072717 .
## month5月:year2005 -0.048398 0.024866 -1.946 0.051771 .
## month6月:year2005 -0.107544 0.025703 -4.184 3.00e-05 ***
## month7月:year2005 -0.135649 0.025259 -5.370 8.90e-08 ***
## month8月:year2005 -0.092462 0.025750 -3.591 0.000339 ***
## month9月:year2005 -0.138531 0.026062 -5.315 1.20e-07 ***
## month10月:year2006 -0.182780 0.025217 -7.248 6.28e-13 ***
## month11月:year2006 -0.116811 0.025223 -4.631 3.90e-06 ***
## month12月:year2006 -0.198415 0.023838 -8.323 < 2e-16 ***
## month1月:year2006 -0.205036 0.022986 -8.920 < 2e-16 ***
## month2月:year2006 -0.026963 0.024750 -1.089 0.276115
## month3月:year2006 -0.040432 0.023497 -1.721 0.085477 .
## month4月:year2006 -0.085812 0.025032 -3.428 0.000622 ***
## month5月:year2006 -0.105046 0.025235 -4.163 3.30e-05 ***
## month6月:year2006 -0.089373 0.025581 -3.494 0.000488 ***
## month7月:year2006 -0.095181 0.024990 -3.809 0.000144 ***
## month8月:year2006 -0.106578 0.025845 -4.124 3.90e-05 ***
## month9月:year2006 -0.160521 0.026217 -6.123 1.13e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 1.385637)
##
## Null deviance: 5129.6 on 1825 degrees of freedom
## Residual deviance: 2413.2 on 1766 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4
# COMPUTE PREDICTED NUMBER OF DEATHS FROM THIS MODEL
pred1 <- predict(model1,type="response")
plot(data$date,data$numdeaths,ylim=c(100,300),pch=19,cex=0.2,col=grey(0.6),
main="Time-stratified model (month strata)",ylab="Daily number of deaths",
xlab="Date")
lines(data$date,pred1,lwd=2)
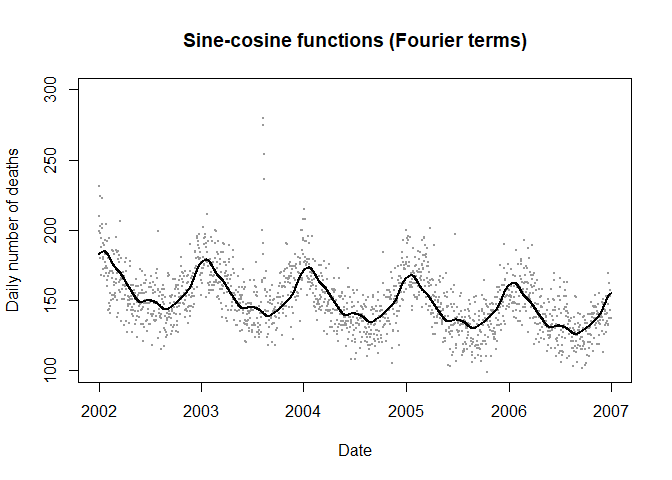
周期函数(Periodic functions–Fourier terms)
长期趋势可以通过在泊松回归中加入傅里叶变换拟合得更为平滑。通过成对的时间正余弦函数来反应完整的季节周期。
优点:通过更少的参数来拟合更为平滑的长期趋势。
缺点:在数学上较时间分层模型复杂;模型中的季节趋势连年相同,可能与时期情况不符。
# OPTION 2: PERIODIC FUNCTIONS MODEL
# (FOURIER TERMS)
# GENERATE FOURIER TERMS
# (USE FUNCTION harmonic, IN PACKAGE tsModel TO BE INSTALLED AND THEN LOADED)
library(tsModel)
## Time Series Modeling for Air Pollution and Health (0.6)
# 4 SINE-COSINE PAIRS REPRESENTING DIFFERENT HARMONICS WITH PERIOD 1 YEAR
data$time <- seq(nrow(data))
fourier <- harmonic(data$time,nfreq=4,period=365.25)
# FIT A POISSON MODEL FOURIER TERMS + LINEAR TERM FOR TREND
# (USE OF quasipoisson FAMILY FOR SCALING THE STANDARD ERRORS)
model2 <- glm(numdeaths ~ fourier + time,data,family=quasipoisson)
summary(model2)
##
## Call:
## glm(formula = numdeaths ~ fourier + time, family = quasipoisson,
## data = data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.6203 -0.8390 -0.0967 0.7338 10.3189
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.084e+00 4.800e-03 1059.155 < 2e-16 ***
## fourier1 4.650e-02 3.486e-03 13.337 < 2e-16 ***
## fourier2 1.573e-02 3.439e-03 4.573 5.14e-06 ***
## fourier3 5.421e-03 3.417e-03 1.587 0.11278
## fourier4 -2.380e-03 3.414e-03 -0.697 0.48594
## fourier5 9.053e-02 3.404e-03 26.592 < 2e-16 ***
## fourier6 2.457e-02 3.412e-03 7.202 8.67e-13 ***
## fourier7 9.808e-03 3.416e-03 2.871 0.00413 **
## fourier8 -1.106e-03 3.414e-03 -0.324 0.74601
## time -8.825e-05 4.657e-06 -18.948 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 1.590869)
##
## Null deviance: 5129.6 on 1825 degrees of freedom
## Residual deviance: 2789.9 on 1816 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4
# COMPUTE PREDICTED NUMBER OF DEATHS FROM THIS MODEL
pred2 <- predict(model2,type="response")
plot(data$date,data$numdeaths,ylim=c(100,300),pch=19,cex=0.2,col=grey(0.6),
main="Sine-cosine functions (Fourier terms)",ylab="Daily number of deaths",
xlab="Date")
lines(data$date,pred2,lwd=2)
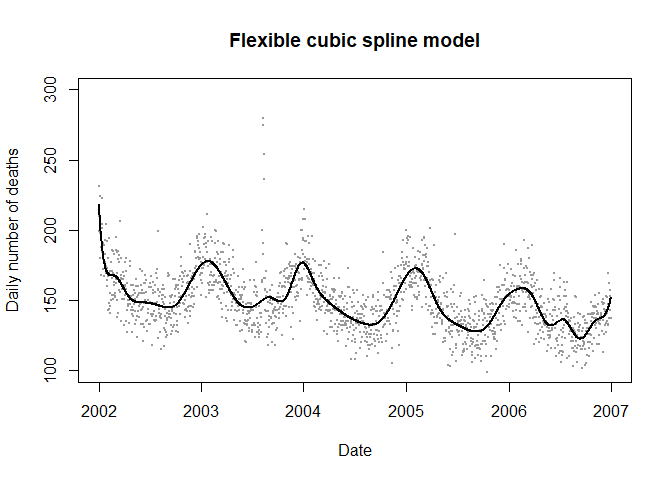
灵活的样条平滑函数(Flexible spline functions)
第三种方法就是在整个研究时间段内加入样条平滑函数(常用的是自然立方样条平滑)。
优点:能平滑的拟合长期趋势;能区别开不同年份各自的季节趋势;同时能识别数据中的长期非季节趋势。
缺点:在数学上较其他方法更为复杂。
# OPTION 3: SPLINE MODEL
# (FLEXIBLE SPLINE FUNCTIONS)
# GENERATE SPLINE TERMS
# (USE FUNCTION bs IN PACKAGE splines, TO BE LOADED)
library(splines)
# A CUBIC B-SPLINE WITH 32 EQUALLY-SPACED KNOTS + 2 BOUNDARY KNOTS
# (NOTE: THIS PARAMETERIZATION IS SLIGHTLY DIFFERENT THAN STATA'S)
# (THE 35 BASIS VARIABLES ARE SET AS df, WITH DEFAULT KNOTS PLACEMENT. SEE ?bs)
# (OTHER TYPES OF SPLINES CAN BE PRODUCED WITH THE FUNCTION ns. SEE ?ns)
spl <- bs(data$time,degree=3,df=35)
# FIT A POISSON MODEL FOURIER TERMS + LINEAR TERM FOR TREND
# (USE OF quasipoisson FAMILY FOR SCALING THE STANDARD ERRORS)
model3 <- glm(numdeaths ~ spl,data,family=quasipoisson)
summary(model3)
##
## Call:
## glm(formula = numdeaths ~ spl, family = quasipoisson, data = data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.6791 -0.7950 -0.0407 0.7092 9.3852
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.38737 0.03486 154.541 < 2e-16 ***
## spl1 -0.31076 0.06697 -4.640 3.73e-06 ***
## spl2 -0.20888 0.04387 -4.762 2.08e-06 ***
## spl3 -0.40118 0.05166 -7.766 1.35e-14 ***
## spl4 -0.37987 0.04382 -8.670 < 2e-16 ***
## spl5 -0.40692 0.04704 -8.650 < 2e-16 ***
## spl6 -0.42251 0.04485 -9.421 < 2e-16 ***
## spl7 -0.27138 0.04512 -6.015 2.18e-09 ***
## spl8 -0.17365 0.04419 -3.930 8.83e-05 ***
## spl9 -0.26489 0.04483 -5.909 4.11e-09 ***
## spl10 -0.41225 0.04535 -9.091 < 2e-16 ***
## spl11 -0.41962 0.04562 -9.199 < 2e-16 ***
## spl12 -0.32815 0.04537 -7.232 7.01e-13 ***
## spl13 -0.43933 0.04523 -9.712 < 2e-16 ***
## spl14 -0.12734 0.04457 -2.857 0.00432 **
## spl15 -0.33645 0.04501 -7.474 1.21e-13 ***
## spl16 -0.39864 0.04565 -8.733 < 2e-16 ***
## spl17 -0.45648 0.04615 -9.891 < 2e-16 ***
## spl18 -0.49703 0.04644 -10.702 < 2e-16 ***
## spl19 -0.51027 0.04630 -11.022 < 2e-16 ***
## spl20 -0.38345 0.04551 -8.425 < 2e-16 ***
## spl21 -0.21867 0.04478 -4.883 1.14e-06 ***
## spl22 -0.23762 0.04491 -5.291 1.36e-07 ***
## spl23 -0.44907 0.04582 -9.802 < 2e-16 ***
## spl24 -0.49518 0.04650 -10.649 < 2e-16 ***
## spl25 -0.54217 0.04681 -11.582 < 2e-16 ***
## spl26 -0.53737 0.04656 -11.542 < 2e-16 ***
## spl27 -0.36096 0.04575 -7.889 5.25e-15 ***
## spl28 -0.31603 0.04537 -6.966 4.57e-12 ***
## spl29 -0.31964 0.04567 -6.999 3.63e-12 ***
## spl30 -0.57260 0.04664 -12.276 < 2e-16 ***
## spl31 -0.40232 0.04730 -8.506 < 2e-16 ***
## spl32 -0.66102 0.04968 -13.306 < 2e-16 ***
## spl33 -0.42073 0.05637 -7.464 1.31e-13 ***
## spl34 -0.48379 0.05801 -8.340 < 2e-16 ***
## spl35 -0.36101 0.05369 -6.724 2.38e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 1.432375)
##
## Null deviance: 5129.6 on 1825 degrees of freedom
## Residual deviance: 2499.7 on 1790 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4
# COMPUTE PREDICTED NUMBER OF DEATHS FROM THIS MODEL
pred3 <- predict(model3,type="response")
plot(data$date,data$numdeaths,ylim=c(100,300),pch=19,cex=0.2,col=grey(0.6),
main="Flexible cubic spline model",ylab="Daily number of deaths",
xlab="Date")
lines(data$date,pred3,lwd=2)
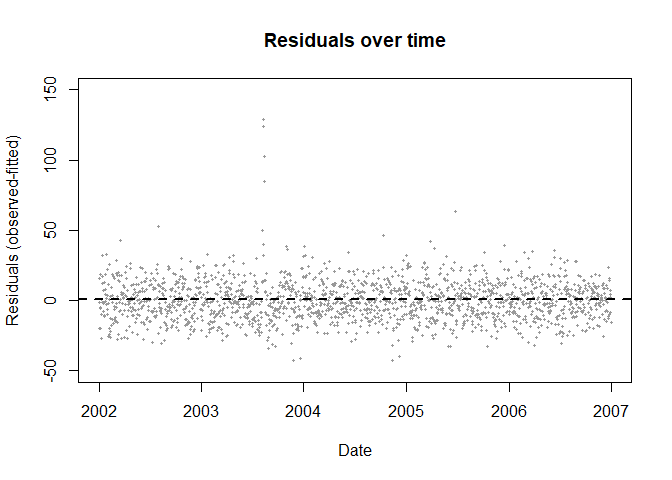
长期趋势下的残差变异
通过上述三种方法控制长期趋势及季节性后,从剩下的残差变异可以看出长期趋势已经不再明显。
# PLOT RESPONSE RESIDUALS OVER TIME
# FROM MODEL 3
# GENERATE RESIDUALS
res3 <- residuals(model3,type="response")
plot(data$date,res3,ylim=c(-50,150),pch=19,cex=0.4,col=grey(0.6),
main="Residuals over time",ylab="Residuals (observed-fitted)",xlab="Date")
abline(h=1,lty=2,lwd=2)
暴露与结局之间的关联及混杂因素
使用该数据,拟合一个简单的泊松回归模型,当只纳入臭氧作为唯一的解释变量,不控制长期趋势及季节性时,可以看出臭氧每升高10μ**g/m3,死亡率相对危险度为0.991(95%CI:0.987 to 0.994, P < 0.001)。
# ESTIMATING OZONE-MORTALITY ASSOCIATION
# COMPARE THE RR (AND CI)
# (COMPUTED WITH THE FUNCTION ci.lin IN PACKAGE Epi, TO BE INSTALLED AND LOADED)
library(Epi)
##
## Attaching package: 'Epi'
## The following object is masked from 'package:base':
##
## merge.data.frame
data$ozone10 <- data$ozone/10
# UNADJUSTED MODEL
model4 <- glm(numdeaths ~ ozone10,data,family=quasipoisson)
summary(model4)
##
## Call:
## glm(formula = numdeaths ~ ozone10, family = quasipoisson, data = data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -4.6058 -1.1692 -0.1195 1.0252 10.2613
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.039768 0.006887 731.820 < 2e-16 ***
## ozone10 -0.009364 0.001766 -5.301 1.29e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 2.831608)
##
## Null deviance: 5129.6 on 1825 degrees of freedom
## Residual deviance: 5049.8 on 1824 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4
(eff4 <- ci.lin(model4,subset="ozone10",Exp=T))
## Estimate StdErr z P exp(Est.) 2.5%
## ozone10 -0.009363689 0.001766441 -5.300877 1.152477e-07 0.99068 0.987256
## 97.5%
## ozone10 0.9941159
但是,从上述内容我们可以看出,臭氧与死亡率之间的关联至少有一部分可由长期趋势及季节性加以解释。因此,通过对长期趋势及季节性的控制,我们可以发现:RR per 10μ**g/m3 = 1.007, 95%CI:1.003 to 1.010, P < 0.001.
# CONTROLLING FOR SEASONALITY (WITH SPLINE AS IN MODEL 3)
model5 <- update(model4,.~.+spl)
summary(model5)
##
## Call:
## glm(formula = numdeaths ~ ozone10 + spl, family = quasipoisson,
## data = data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.7422 -0.7971 -0.0281 0.7157 8.9675
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.394524 0.034628 155.785 < 2e-16 ***
## ozone10 0.006608 0.001599 4.133 3.74e-05 ***
## spl1 -0.357002 0.067365 -5.300 1.30e-07 ***
## spl2 -0.227264 0.043818 -5.187 2.38e-07 ***
## spl3 -0.448092 0.052521 -8.532 < 2e-16 ***
## spl4 -0.413019 0.044239 -9.336 < 2e-16 ***
## spl5 -0.435182 0.047200 -9.220 < 2e-16 ***
## spl6 -0.446916 0.044926 -9.948 < 2e-16 ***
## spl7 -0.286102 0.044935 -6.367 2.44e-10 ***
## spl8 -0.199243 0.044294 -4.498 7.29e-06 ***
## spl9 -0.289330 0.044890 -6.445 1.48e-10 ***
## spl10 -0.461361 0.046559 -9.909 < 2e-16 ***
## spl11 -0.458090 0.046242 -9.906 < 2e-16 ***
## spl12 -0.368889 0.046122 -7.998 2.25e-15 ***
## spl13 -0.452845 0.045018 -10.059 < 2e-16 ***
## spl14 -0.151914 0.044647 -3.403 0.000682 ***
## spl15 -0.362700 0.045142 -8.035 1.69e-15 ***
## spl16 -0.434286 0.046127 -9.415 < 2e-16 ***
## spl17 -0.490948 0.046560 -10.545 < 2e-16 ***
## spl18 -0.531890 0.046871 -11.348 < 2e-16 ***
## spl19 -0.546444 0.046798 -11.677 < 2e-16 ***
## spl20 -0.389140 0.045204 -8.609 < 2e-16 ***
## spl21 -0.253212 0.045219 -5.600 2.48e-08 ***
## spl22 -0.259292 0.044872 -5.778 8.88e-09 ***
## spl23 -0.491057 0.046595 -10.539 < 2e-16 ***
## spl24 -0.536585 0.047235 -11.360 < 2e-16 ***
## spl25 -0.567940 0.046889 -12.112 < 2e-16 ***
## spl26 -0.566718 0.046770 -12.117 < 2e-16 ***
## spl27 -0.375020 0.045558 -8.232 3.52e-16 ***
## spl28 -0.336118 0.045306 -7.419 1.82e-13 ***
## spl29 -0.366222 0.046707 -7.841 7.63e-15 ***
## spl30 -0.606314 0.047016 -12.896 < 2e-16 ***
## spl31 -0.456894 0.048773 -9.368 < 2e-16 ***
## spl32 -0.679548 0.049512 -13.725 < 2e-16 ***
## spl33 -0.447328 0.056359 -7.937 3.62e-15 ***
## spl34 -0.512691 0.057949 -8.847 < 2e-16 ***
## spl35 -0.383634 0.053517 -7.169 1.10e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 1.414007)
##
## Null deviance: 5129.6 on 1825 degrees of freedom
## Residual deviance: 2475.5 on 1789 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4
(eff5 <- ci.lin(model5,subset="ozone10",Exp=T))
## Estimate StdErr z P exp(Est.) 2.5%
## ozone10 0.006608467 0.001598843 4.133281 3.576213e-05 1.00663 1.003481
## 97.5%
## ozone10 1.00979
进一步控制其他混杂因素
从上面的结果可以看出,在控制长期趋势及季节性后,臭氧与死亡率之间存在正性相关。哪是否还有其他的混杂因素呢?一般流行病学研究中,常见的混杂因素有年龄、性别、BMI、吸烟、饮酒等,但是这些“标准混杂”因素在本数据中并不存在,因为在人群水平中,这些因素不会或者不大可能每日改变,或者随着环境暴露因素不同水平而发生波动。那么,在本研究中,在人群水平上,逐日改变,并可能与臭氧、死亡率波动发生关联的则是温度。通过进一步控制温度,我们可以发现:RR per 10μ**g/m3 = 1.003, 95%CI:0.999 to 1.006, P = 0.11.这表明,上述臭氧与死亡率之间的正性关系很大部分是由温度这个混杂因素引起的。
# CONTROLLING FOR TEMPERATURE
# (TEMPERATURE MODELLED WITH CATEGORICAL VARIABLES FOR DECILES)
# (MORE SOPHISTICATED APPROACHES ARE AVAILABLE - SEE ARMSTRONG EPIDEMIOLOGY 2006)
cutoffs <- quantile(data$temperature,probs=0:10/10)
tempdecile <- cut(data$temperature,breaks=cutoffs,include.lowest=TRUE)
model6 <- update(model5,.~.+tempdecile)
summary(model6)
##
## Call:
## glm(formula = numdeaths ~ ozone10 + spl + tempdecile, family = quasipoisson,
## data = data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.4749 -0.7592 -0.0325 0.6998 8.6310
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.397434 0.033885 159.289 < 2e-16 ***
## ozone10 0.002660 0.001650 1.613 0.106982
## spl1 -0.355647 0.066453 -5.352 9.83e-08 ***
## spl2 -0.215023 0.042925 -5.009 6.01e-07 ***
## spl3 -0.449535 0.052067 -8.634 < 2e-16 ***
## spl4 -0.416087 0.045145 -9.217 < 2e-16 ***
## spl5 -0.516694 0.049237 -10.494 < 2e-16 ***
## spl6 -0.437726 0.045604 -9.598 < 2e-16 ***
## spl7 -0.299331 0.044730 -6.692 2.94e-11 ***
## spl8 -0.185173 0.043329 -4.274 2.02e-05 ***
## spl9 -0.289821 0.044665 -6.489 1.12e-10 ***
## spl10 -0.443079 0.046972 -9.433 < 2e-16 ***
## spl11 -0.550633 0.048016 -11.468 < 2e-16 ***
## spl12 -0.412416 0.047248 -8.729 < 2e-16 ***
## spl13 -0.443119 0.044840 -9.882 < 2e-16 ***
## spl14 -0.153709 0.043806 -3.509 0.000461 ***
## spl15 -0.349490 0.044111 -7.923 4.05e-15 ***
## spl16 -0.434906 0.045638 -9.530 < 2e-16 ***
## spl17 -0.492358 0.047545 -10.356 < 2e-16 ***
## spl18 -0.632479 0.048350 -13.081 < 2e-16 ***
## spl19 -0.554391 0.047527 -11.665 < 2e-16 ***
## spl20 -0.399647 0.044679 -8.945 < 2e-16 ***
## spl21 -0.236988 0.044409 -5.336 1.07e-07 ***
## spl22 -0.260740 0.043819 -5.950 3.21e-09 ***
## spl23 -0.477714 0.046766 -10.215 < 2e-16 ***
## spl24 -0.594973 0.048102 -12.369 < 2e-16 ***
## spl25 -0.628064 0.048007 -13.083 < 2e-16 ***
## spl26 -0.580350 0.047597 -12.193 < 2e-16 ***
## spl27 -0.368372 0.044714 -8.238 3.34e-16 ***
## spl28 -0.332371 0.044260 -7.510 9.33e-14 ***
## spl29 -0.349631 0.045895 -7.618 4.16e-14 ***
## spl30 -0.618523 0.048199 -12.833 < 2e-16 ***
## spl31 -0.549227 0.049455 -11.106 < 2e-16 ***
## spl32 -0.712232 0.051275 -13.891 < 2e-16 ***
## spl33 -0.454224 0.055707 -8.154 6.58e-16 ***
## spl34 -0.503764 0.057161 -8.813 < 2e-16 ***
## spl35 -0.379877 0.052373 -7.253 6.04e-13 ***
## tempdecile(4,6.44] 0.001244 0.009769 0.127 0.898711
## tempdecile(6.44,8.27] -0.010651 0.010343 -1.030 0.303273
## tempdecile(8.27,10] 0.015512 0.010701 1.450 0.147340
## tempdecile(10,11.5] 0.018312 0.011711 1.564 0.118059
## tempdecile(11.5,13.3] 0.013201 0.012743 1.036 0.300404
## tempdecile(13.3,15.3] 0.027105 0.014409 1.881 0.060116 .
## tempdecile(15.3,17] 0.034276 0.015695 2.184 0.029104 *
## tempdecile(17,18.9] 0.038294 0.016604 2.306 0.021208 *
## tempdecile(18.9,28.2] 0.119680 0.017702 6.761 1.85e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 1.345358)
##
## Null deviance: 5129.6 on 1825 degrees of freedom
## Residual deviance: 2351.7 on 1780 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4
(eff6 <- ci.lin(model6,subset="ozone10",Exp=T))
## Estimate StdErr z P exp(Est.) 2.5%
## ozone10 0.002660343 0.001649596 1.612724 0.1068044 1.002664 0.9994274
## 97.5%
## ozone10 1.005911
# BUILD A SUMMARY TABLE WITH EFFECT AS PERCENT INCREASE
tabeff <- rbind(eff4,eff5,eff6)[,5:7]
tabeff <- (tabeff-1)*100
dimnames(tabeff) <- list(c("Unadjusted","Plus season/trend","Plus temperature"),
c("RR","ci.low","ci.hi"))
round(tabeff,2)
## RR ci.low ci.hi
## Unadjusted -0.93 -1.27 -0.59
## Plus season/trend 0.66 0.35 0.98
## Plus temperature 0.27 -0.06 0.59
另外,其他混杂因素还有相对湿度、其他污染物、星期几效应和节假日效应等。这里不再一一讨论。
探讨暴露因素的滞后效应
至目前为止,我们讨论了当日臭氧与当日死亡率之间的关联。暴露与结局之间是否可能存在滞后效应,则是需要进一步考虑的问题。即“昨日”的臭氧是否与“今日”的死亡率相关。
# EXPLORING THE LAGGED (DELAYED) EFFECTS
# SINGLE-LAG MODELS
# PREPARE THE TABLE WITH ESTIMATES
tablag <- matrix(NA,7+1,3,dimnames=list(paste("Lag",0:7),
c("RR","ci.low","ci.hi")))
# RUN THE LOOP
for(i in 0:7) {
# LAG OZONE AND TEMPERATURE VARIABLES
ozone10lag <- Lag(data$ozone10,i)
tempdecilelag <- cut(Lag(data$temperature,i),breaks=cutoffs,
include.lowest=TRUE)
# DEFINE THE TRANSFORMATION FOR TEMPERATURE
# LAG SAME AS ABOVE, BUT WITH STRATA TERMS INSTEAD THAN LINEAR
mod <- glm(numdeaths ~ ozone10lag + tempdecilelag + spl,data,
family=quasipoisson)
tablag[i+1,] <- ci.lin(mod,subset="ozone10lag",Exp=T)[5:7]
}
tablag
## RR ci.low ci.hi
## Lag 0 1.002664 0.9994274 1.005911
## Lag 1 1.007482 1.0042176 1.010756
## Lag 2 1.008195 1.0049222 1.011479
## Lag 3 1.006503 1.0032115 1.009805
## Lag 4 1.005188 1.0018610 1.008527
## Lag 5 1.004218 1.0008532 1.007594
## Lag 6 1.000517 0.9971563 1.003890
## Lag 7 1.000013 0.9966491 1.003389
plot(0:7,0:7,type="n",ylim=c(0.99,1.03),main="Lag terms modelled one at a time",
xlab="Lag (days)",ylab="RR and 95%CI per 10ug/m3 ozone increase")
abline(h=1)
arrows(0:7,tablag[,2],0:7,tablag[,3],length=0.05,angle=90,code=3)
points(0:7,tablag[,1],pch=19)
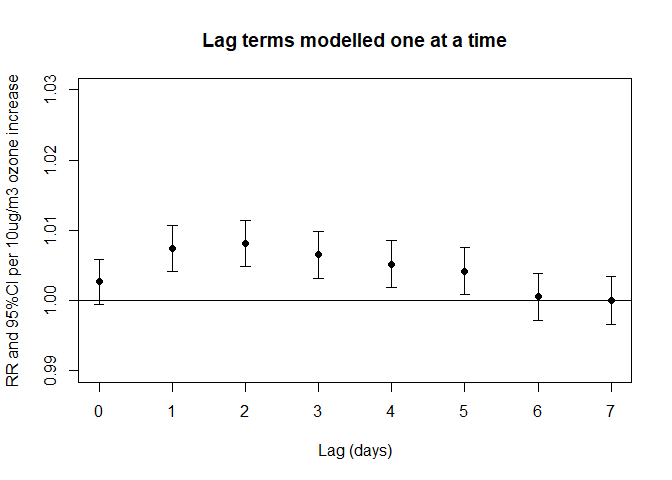
通过上述的单日滞后分析可以发现,在单日之后1 to 5 天,臭氧与死亡率之间存在明显的相关。但是这些单日滞后效应只是分别纳入模型,并没有相互调整。这时,可采用分布滞后模型将这些单日滞后变量(lag0 to lag7)同时纳入模型。
# UNCONSTRAINED DLM
library(dlnm)
## This is dlnm 2.3.2. For details: help(dlnm) and vignette('dlnmOverview').
# IN PARTICULAR, THE FUNCTION crossbasis PRODUCES THE TRANSFORMATION FOR
# SPECIFIC LAG STRUCTURES AND OPTIONALLY FOR NON-LINEARITY
# THE FUNCTION crosspred INSTEAD PREDICTS ESTIMATED EFFECTS
# PRODUCE THE CROSS-BASIS FOR OZONE (SCALING NOT NEEDED)
# A SIMPLE UNSTRANSFORMED LINEAR TERM AND THE UNCONSTRAINED LAG STRUCTURE
cbo3unc <- crossbasis(data$ozone,lag=c(0,7),argvar=list(type="lin",cen=FALSE),
arglag=list(type="integer"))
## Warning in checkcrossbasis(argvar, arglag, list(...)): argument 'type'
## replaced by 'fun'. See ?onebasis
## Warning in checkcrossbasis(argvar, arglag, list(...)): argument 'type'
## replaced by 'fun'. See ?onebasis
## Warning in checkonebasis(fun, args, cen): centering through 'cen' now
## applied at the prediction stage. See ?crosspred
summary(cbo3unc)
## CROSSBASIS FUNCTIONS
## observations: 1826
## range: 1.181818 to 119.2457
## lag period: 0 7
## total df: 8
##
## BASIS FOR VAR:
## fun: lin
## intercept: FALSE
##
## BASIS FOR LAG:
## fun: integer
## values: 0 1 2 3 4 5 6 ...
## intercept: TRUE
# PRODUCE THE CROSS-BASIS FOR TEMPERATURE
# AS ABOVE, BUT WITH STRATA DEFINED BY INTERNAL CUT-OFFS
cbtempunc <- crossbasis(data$temperature,lag=c(0,7),
argvar=list(type="strata",knots=cutoffs[2:10]),
arglag=list(type="integer"))
## Warning in checkcrossbasis(argvar, arglag, list(...)): argument 'type'
## replaced by 'fun'. See ?onebasis
## Warning in checkcrossbasis(argvar, arglag, list(...)): argument 'type'
## replaced by 'fun'. See ?onebasis
## Warning in checkonebasis(fun, args, cen): argument 'knots' replaced by
## 'breaks' in function strata. See ?strata
summary(cbtempunc)
## CROSSBASIS FUNCTIONS
## observations: 1826
## range: -1.400507 to 28.175
## lag period: 0 7
## total df: 72
##
## BASIS FOR VAR:
## fun: strata
## df: 9
## breaks: 4.003125 6.44375 8.271222 10.01869 11.47275 13.34375 15.27115 ...
## ref: 1
## intercept: FALSE
##
## BASIS FOR LAG:
## fun: integer
## values: 0 1 2 3 4 5 6 ...
## intercept: TRUE
# RUN THE MODEL AND OBTAIN PREDICTIONS FOR OZONE LEVEL 10ug/m3
model7 <- glm(numdeaths ~ cbo3unc + cbtempunc + spl,data,family=quasipoisson)
pred7 <- crosspred(cbo3unc,model7,at=10)
# ESTIMATED EFFECTS AT EACH LAG
tablag2 <- with(pred7,t(rbind(matRRfit,matRRlow,matRRhigh)))
colnames(tablag2) <- c("RR","ci.low","ci.hi")
tablag2
## RR ci.low ci.hi
## lag0 0.9998301 0.9961204 1.003554
## lag1 1.0066534 1.0022830 1.011043
## lag2 1.0046525 1.0002397 1.009085
## lag3 1.0015800 0.9971671 1.006012
## lag4 1.0011224 0.9967088 1.005555
## lag5 1.0014855 0.9970741 1.005916
## lag6 0.9982712 0.9939150 1.002647
## lag7 1.0007098 0.9969463 1.004488
# OVERALL CUMULATIVE (NET) EFFECT
pred7$allRRfit ; pred7$allRRlow ; pred7$allRRhigh
## 10
## 1.01437
## 10
## 1.007994
## 10
## 1.020786
plot(pred7,var=10,type="p",ci="bars",col=1,pch=19,ylim=c(0.99,1.03),
main="All lag terms modelled together (unconstrained)",xlab="Lag (days)",
ylab="RR and 95%CI per 10ug/m3 ozone increase")
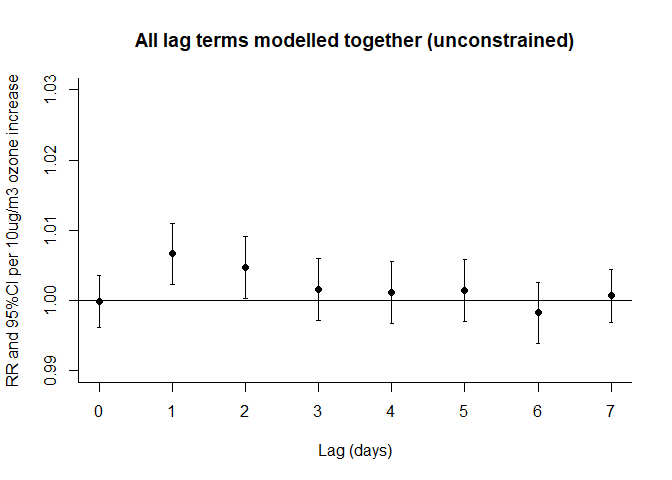
该结果与独立单日滞后相比,可发现独立滞后(lag0 to lag5)的效应已趋向1,表明独立滞后效应收到相互的混杂影响。从结果上看,臭氧与死亡率仅在lag1 和lag2 存在明显的相关,表明当日的死亡率与前两天的臭氧存在正性相关,或者说当日的臭氧与接下来两天的死亡率存在正性相关。
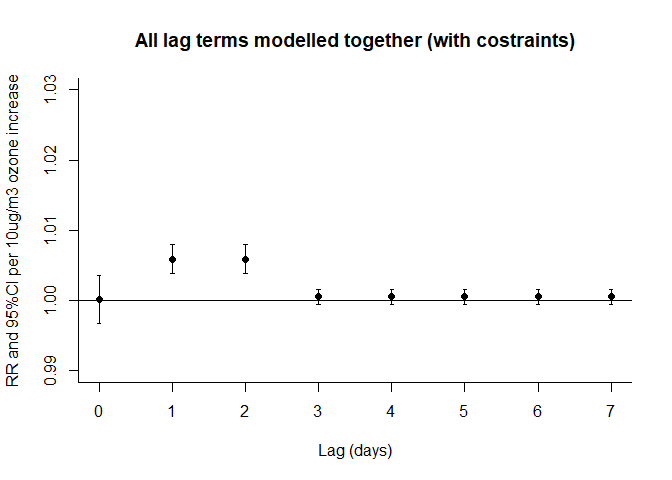
这种不受约束的分布滞后模型可能存在高度的自相关,滞后项之间的共线性可能使模型结果不准确。通过滞后分层分布滞后模型,即将lag1 and lag2的效应视为相同,lag3 to lag7的效应也视为相同。这样处理后,共线性大量减少,需要评估的参数也变少,滞后效应也能更为准确的评估。约束条件的选择也可以更为复杂,如加入平滑函数(多项式或样条函数)。
# CONSTRAINED (LAG-STRATIFIED) DLM
# PRODUCE A DIFFERENT CROSS-BASIS FOR OZONE
# USE STRATA FOR LAG STRUCTURE, WITH CUT-OFFS DEFINING RIGHT-OPEN INTERVALS
cbo3constr <- crossbasis(data$ozone,lag=c(0,7),argvar=list(type="lin",cen=FALSE),
arglag=list(type="strata",knots=c(1,3)))
## Warning in checkcrossbasis(argvar, arglag, list(...)): argument 'type'
## replaced by 'fun'. See ?onebasis
## Warning in checkcrossbasis(argvar, arglag, list(...)): argument 'type'
## replaced by 'fun'. See ?onebasis
## Warning in checkonebasis(fun, args, cen): centering through 'cen' now
## applied at the prediction stage. See ?crosspred
## Warning in checkonebasis(fun, args, cen): argument 'knots' replaced by
## 'breaks' in function strata. See ?strata
summary(cbo3constr)
## CROSSBASIS FUNCTIONS
## observations: 1826
## range: 1.181818 to 119.2457
## lag period: 0 7
## total df: 3
##
## BASIS FOR VAR:
## fun: lin
## intercept: FALSE
##
## BASIS FOR LAG:
## fun: strata
## df: 3
## breaks: 1 3
## ref: 1
## intercept: TRUE
# RUN THE MODEL AND OBTAIN PREDICTIONS FOR OZONE LEVEL 10ug/m3
model8 <- glm(numdeaths ~ cbo3constr + cbtempunc + spl,data,family=quasipoisson)
pred8 <- crosspred(cbo3constr,model8,at=10)
# ESTIMATED EFFECTS AT EACH LAG
tablag3 <- with(pred8,t(rbind(matRRfit,matRRlow,matRRhigh)))
colnames(tablag3) <- c("RR","ci.low","ci.hi")
tablag3
## RR ci.low ci.hi
## lag0 1.000159 0.9967305 1.003599
## lag1 1.005880 1.0038254 1.007938
## lag2 1.005880 1.0038254 1.007938
## lag3 1.000516 0.9994934 1.001540
## lag4 1.000516 0.9994934 1.001540
## lag5 1.000516 0.9994934 1.001540
## lag6 1.000516 0.9994934 1.001540
## lag7 1.000516 0.9994934 1.001540
# OVERALL CUMULATIVE (NET) EFFECT
pred8$allRRfit ; pred8$allRRlow ; pred8$allRRhigh
## 10
## 1.01457
## 10
## 1.00827
## 10
## 1.02091
plot(pred8,var=10,type="p",ci="bars",col=1,pch=19,ylim=c(0.99,1.03),
main="All lag terms modelled together (with costraints)",xlab="Lag (days)",
ylab="RR and 95%CI per 10ug/m3 ozone increase")
模型检验及敏感性分析
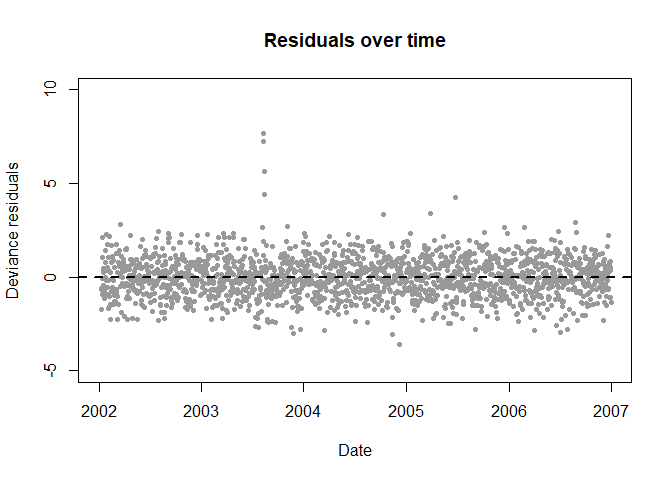
建立完模型后,绘制残差图及做敏感性分析是发现模型假设、数据异常、残差自相关及结果敏感性是否存在问题的必要措施。
# MODEL CHECKING
res7 <- residuals(model7,type="deviance")
plot(data$date,res7,ylim=c(-5,10),pch=19,cex=0.7,col=grey(0.6),
main="Residuals over time",ylab="Deviance residuals",xlab="Date")
abline(h=0,lty=2,lwd=2)
pacf(res7,na.action=na.omit,main="From original model")
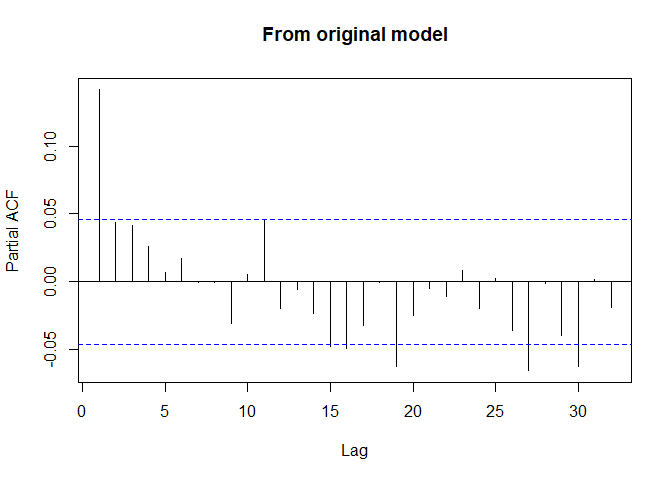
# INCLUDE THE 1-DAY LAGGED RESIDUAL IN THE MODEL
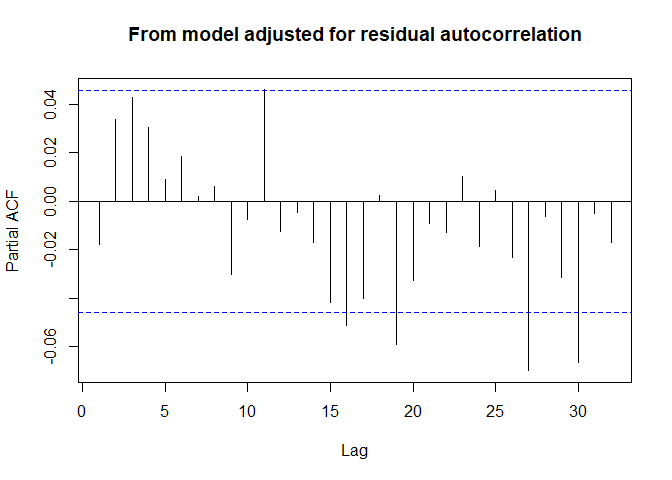
model9 <- update(model7,.~.+Lag(res7,1))
pacf(residuals(model9,type="deviance"),na.action=na.omit,
main="From model adjusted for residual autocorrelation")
精度与效能
据悉,效能计算的方法并非完善。但是我们可知的是时间序列的长度及发生结局效应的人数都能决定研究精度,结局效应的人数过度离散也对精度有所影响。以笔者的经验来看,研究污染物的健康效应,通常数千观测天数,结局数达到数十每天时,模型的精度和效能是可信的。
总结
时间序列分析的基本思路:
1. Explore data with simple plots and tabulations:
a). Plot of exposure variable(s) against time
b). Plot of outcome against time
c). Correlation matrix for exposure and outcome variables
d). Summary statistics for each variable
e). Summary of missing data in each variable
2. Methods to control for seasonality and long-term trends:
a). Indicator variables for time strata (time-stratified model)
b). Periodic functions of time (sine/cosine functions)
c). Flexible spline functions of time.
3. Modelling the exposure-outcome association—immediate vs delayed effects
a). Individual lag models considering different lags one at a time
b). Distributed lag models considering all lags in a single model (unconstrained, or constrained to reduce collinearity)
c). Consider possible non-linear associations as in other regression contexts.
4. Model checking
a). Diagnostic plots based on deviance residuals
b). Multiple sensitivity analyses changing key modelling decisions
扩展
暴露-结局之间的非线性关联
暴露因素与其他混杂因素都可能与结局之间存在非线性关系,这时可采用分类变量、二次或高阶多项式、样条平滑曲线或分段线性阈值模型。
修饰效应
个体水平的因素也可能存在修饰效应,如老年人是否对臭氧更为敏感?若是能确定结局变量中不同层次的数目,则可以进一步探讨这种修饰效应。
多中心研究
以地区进行单独分析可增加模型效能,同时能提供环境暴露因素更多的异质性。多中心的研究可采用meta分析的方法进行类推,或者以地区进行分层建模。