相关关系是一种研究随机变量间相关关系的统计方法。散点图和相关图是常见的相关分析方法。
散点图
散点图矩阵
下面以R自带数据集iris为例,分析Sepal.Length,Sepal.Width,Petal.Length和Petal.Width四个变量之间的关系。使用pairs()函数绘制散点图矩阵,代码如下:
pairs(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,data = iris,
main = "散点图矩阵")
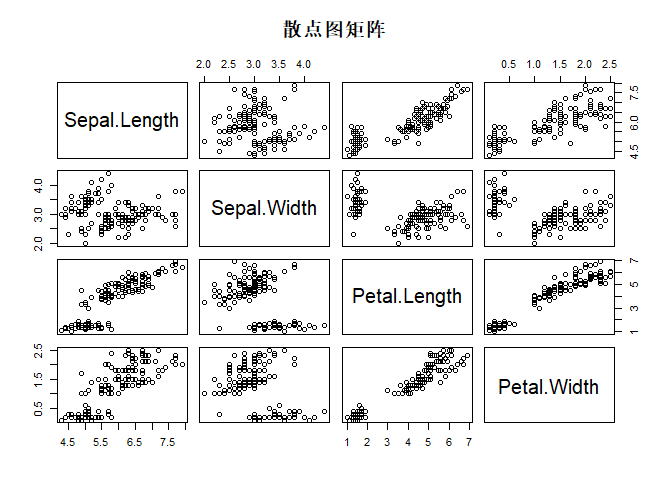
通过散点图帐数据分布,可以看出Petal.Length和Petal.Width二者之间的相关性较强。
library(car)
scatterplotMatrix(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width|Species,data = iris)
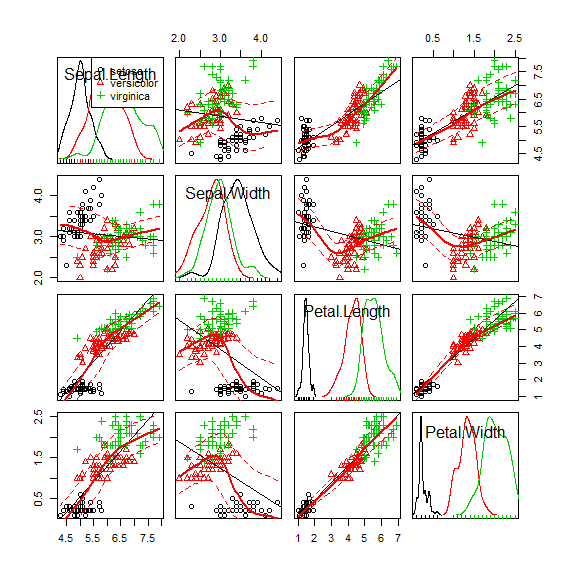
相关图
将不同变量之间的相关关系通过可视化的方法展示出来即相关图。
相关矩阵图
corrgram中的corrgram()函数和corrplot包中的corrplot()函数均可绘制相关矩阵图。一般用法如下所示:
library(corrgram)
# 1、排序处理
corrgram(mtcars,order = TRUE)
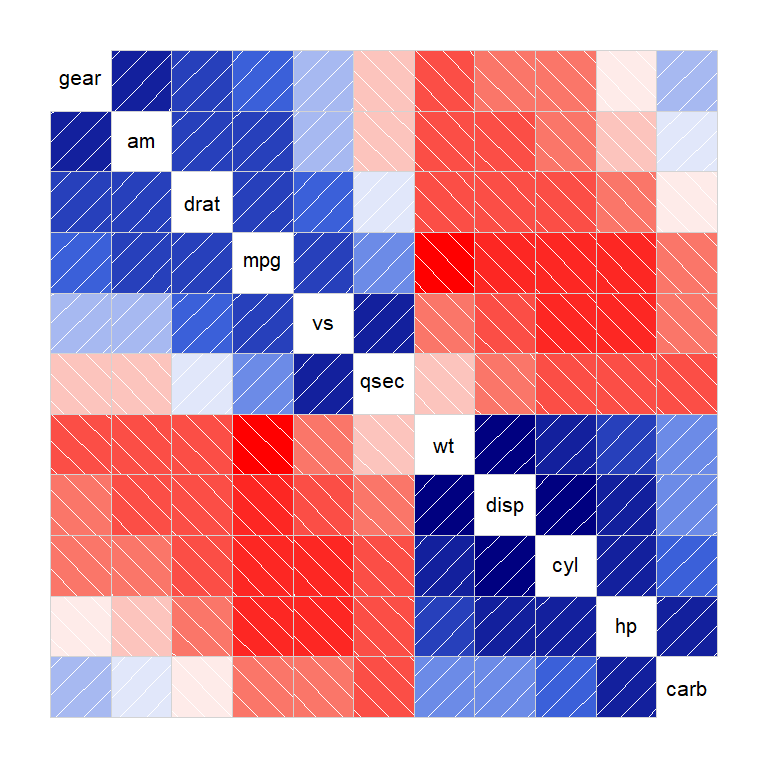
# 2、设置三角面板形状
corrgram(mtcars,order = TRUE, lower.panel = panel.shade,upper.panel = panel.pie)

# 3、只显示下三角面板
corrgram(mtcars,order = TRUE, lower.panel = panel.shade,upper.panel = NULL)
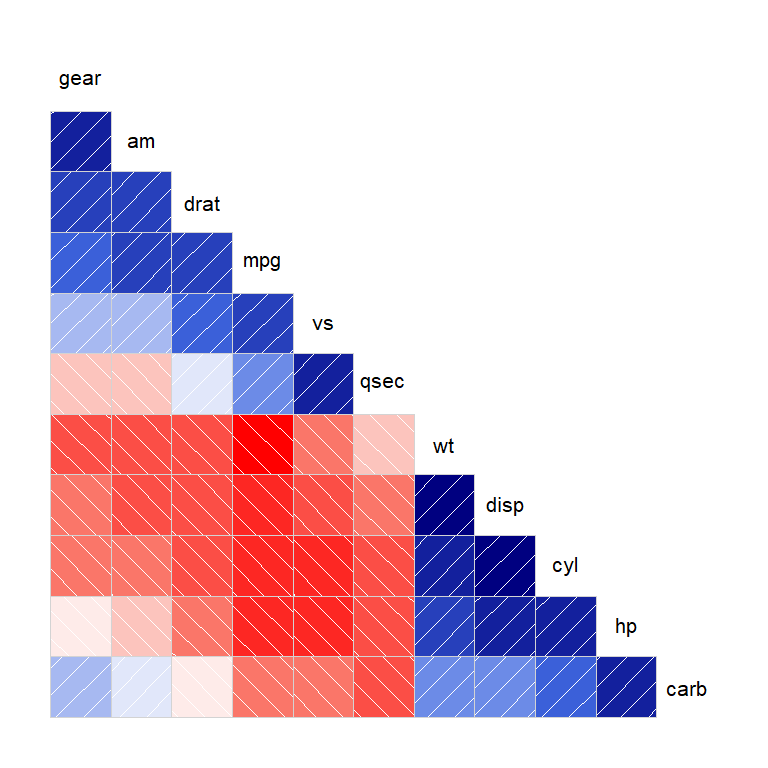
# 4、调整面板颜色
corrgram(mtcars,order = TRUE, lower.panel = panel.shade,upper.panel = panel.pie,
col.regions = colorRampPalette(c("darkgoldenrod4","burlywood1","white",
"darkkhaki","darkgreen")))

使用corrplot()函数绘制的示例如下:
library(corrplot)
# 1、使用不同的method绘制相关矩阵图
methods <- c("circle","square","ellipse","pie","shade","color")
par(mfrow = c(2,3))
M <- cor(mtcars)
t0 <- mapply(function(x){corrplot(M, method = x, order = "AOE")},methods)
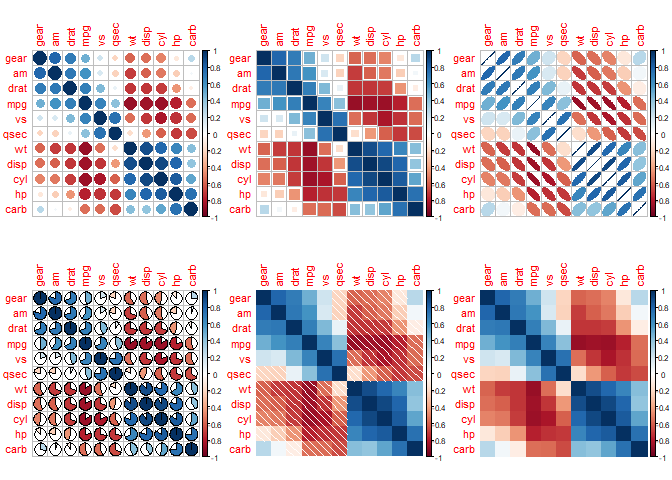
par(mfrow = c(1,1))
# 2、设置method = color 绘制热力矩阵图
corrplot(cor(mtcars), method = "color", order = "AOE", tl.col = "black",
tl.srt = 45, addCoef.col = "black",
col = colorRampPalette(c("#7F0000","red","#FF7F00","yellow","white",
"cyan","#007FFF","blue","#00007F"))(20))
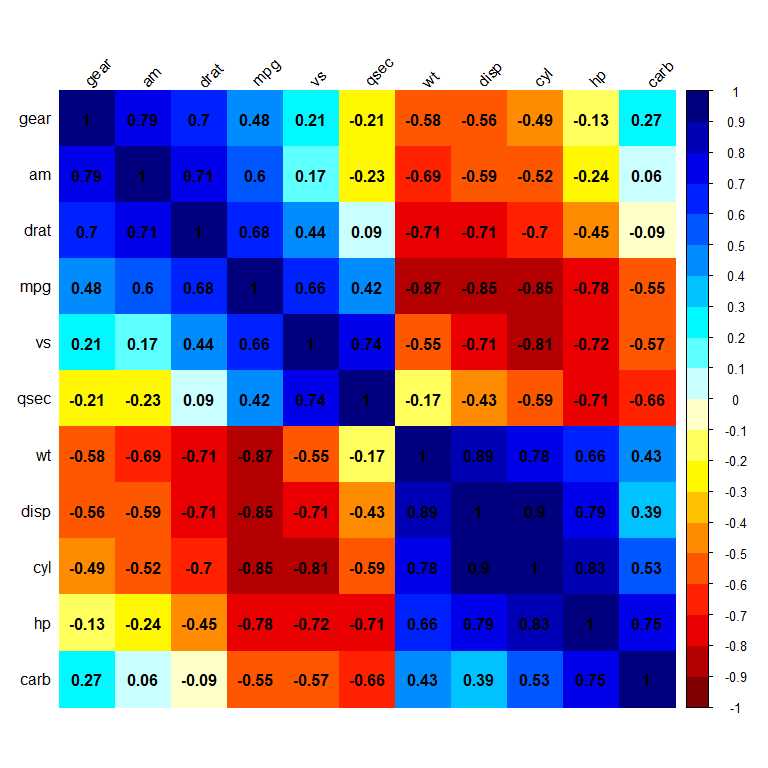
# 3、绘制上下三角及不同色彩的相关矩阵图
library(RColorBrewer)
par(mfrow = c(2,2))
corrplot(cor(mtcars),type = "lower")
corrplot(cor(mtcars),type = "lower", order = "hclust",
col = brewer.pal(n=8, name = "RdYlBu"))
corrplot(cor(mtcars),type = "upper", order = "AOE",
col = c("black","white"),bg = "lightblue")
corrplot(cor(mtcars),type = "upper", order = "FPC",
col = brewer.pal(n=8, name = "PuOr"))
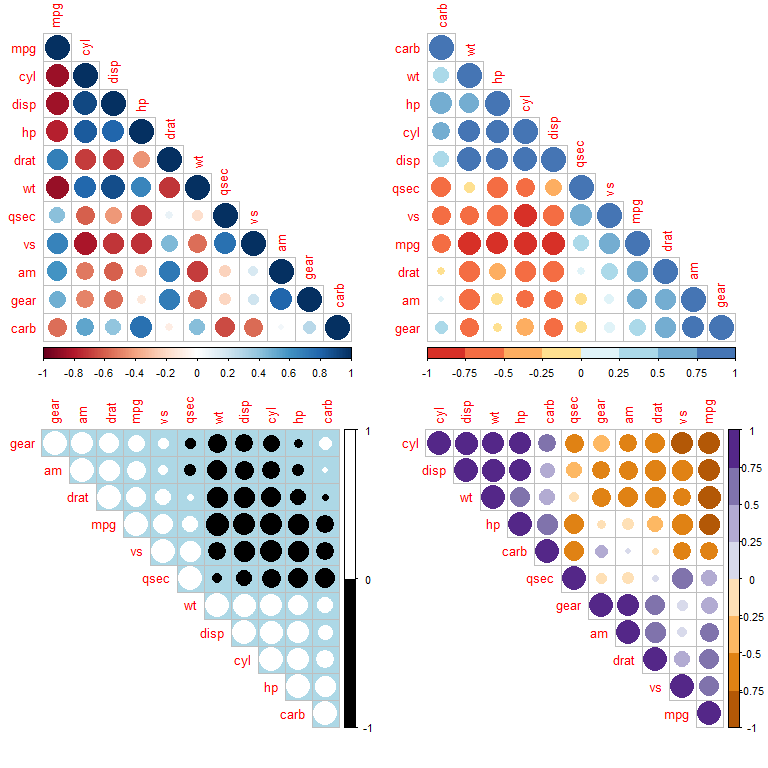
par(mfrow = c(1,1))